R ile Enerji Analizi – Bölüm 4 – Verileri Bileşenlerine Ayırmak

 

Özet: Bu bölümde daha önceki çalışmalarımızın üzerine, verileri bileşenlerine ayırmaya çalışacağız. Basit bir doğrusal regresyon ve bir de decompose komutunu deneyeceğiz

Bu Bölümdeki Fonksiyonlar

read.csv

plot(veri, pch=<veri noktası karakter no>, cex=<karakter büyüklüğü>,col=”renk”)

lm(y~x)

abline(<regresyon sonucu>)

hist(<veri>)

points(<plot gibi ama plot’dan sonra nokta çizer>)

ts(<veri>, frequency=<veri frekansı>, start=<Başladığı tarih>)

decompose (<parçalalara ayırılacak ZAMAN SERİSİ>)

 

4.0. Veriyi yüklemek

Her zamanki gibi veri dosyamızı tekrar yükleyelim.

veri=read.csv("http://www.barissanli.com/calismalar/dersler/r/elektrik-talep.csv", header=TRUE,sep=";",dec=".")

Artık veri dosyamız  R Studio’dan erişilebilir.

4.1. Veriyi bir görelim

Verimizdeki ortalama_tuketim verisine bir göz atalım. Ortalama_tuketim verisi, tüm gün saat saat alınmış elektrik tüketim verisinin toplamının 24’e bölümü ile elde edilmiştir. Elektriğin ilginç bir özelliği var, her an için üretim ve tüketim dengelenmek zorundadır. Bu yüzden anlık tüketim daima, o anda üreten tüm santrallerin üretimleri toplanarak elde edilebilir. Zaten ortalama_tuketim’i 24 ile çarparsak da günlük_tuketim verisini elde ederiz.

Niye böyle bir veriye ihtiyacımız var? Puant (anlık/saatlik en yüksek tüketim) ile kıyaslamak için.

Daha önceki derslerde olduğu gibi,

veri$ortalama_tuketim

ile veriye erişebiliriz. Daha doğrusu “veri”’nin içindeki “ortalama_tuketim” sütununa erişim yapıyoruz. Bunu da daha önce öğrendiğimiz gibi plot fonksiyonu ile çizelim.

plot(veri$ortalama_tuketim, pch=19,cex=0.6,col="#00008822")

 

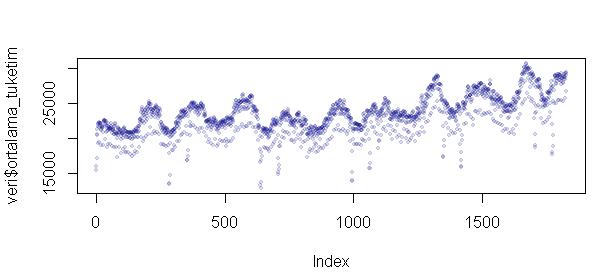
Veriye şöyle bir göz atarsak, tekrar eden bir azalıp azalan sinüs/kosinüs’leri var gibi gözüküyor. Biz buna mevsimsellik diyoruz. Bir de sanki sürekli artan bir doğrunun üzerinde hareket ediyormuş gibi gözüküyor, buna da tüketimin “trend”’i diyelim.

Sorumuz şu : “hem trendi hem mevsimselliği olan bu veriyi nasıl bileşenlerine ayırabiliriz.

4.2. Önce zor olan: Doğrusal regresyon ile trend’i ayıklamak

Filtreleme tek başına pek bir anlam taşımıyor olabilir, bunun için önce bir soruya filtreleme ile cevap arayalım. Bu kısımda amacımız doğrusal regresyonla, birçok data noktasına en yakından geçen doğruyu bulmaya çalışacağız.

Bunun için adım adım,

1.      Önce verimizi normal hali ile çizeceğiz

2.      Sonra her seferinde uzun uzun “veri$ortalama_tuketim” yazmamak için “ot” değişkenine atama yapacağız

3.      Verimizi, verimizin indeksine göre doğrusal regresyona tutacağız. Regresyon sonucumuz, eğilim eğrisi (tüm noktaların en yakınından geçen doğru parçası olacak)

4.      Bu eğriyi, daha önceki plot’umuzun üzerine “abline” komutu ile çizdireceğiz.

5.      Elimizde kalan residual/tortu/kalıntıda trend’den ayıklanmış veriler olacak

Þimdi çizelim:

plot(veri$ortalama_tuketim, pch=19,cex=0.6,col="#00008822")

ot=veri$ortalama_tuketim

regres=lm(ot~time(ot))

abline(regres)

 

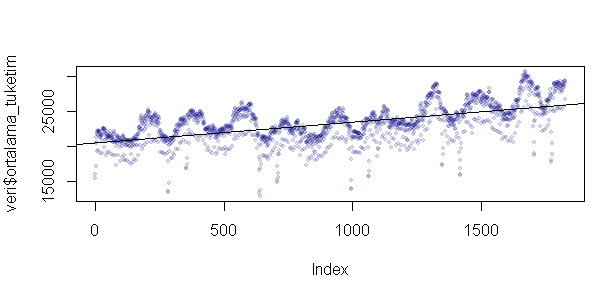
Görüldüğü üzere verimizin devam eden bir trendini bulduk ve üzerine çizdirdik, bu veri serisi durağan/stationary değil diyebiliriz.

 

Peki “lm” komutu ne iş yapar?

lm komutunun özelliklerini ?lm yazarak öğrenebilirsiniz.

lm komutunun içine y ve x değerlerinizi vererek m ve a’yı hesaplar. Burada m eğim(slope), a ise kesme noktası (intercept) “y=mx+a”  formülüne uygun şekilde bulmak için

lm(y~x)

yazarız ve R bize regresyon çıktısını verir.

Peki eğrimizin eğilimi ne? Bunun için “regres” yazarak verilerimizi görebiliriz.

regres

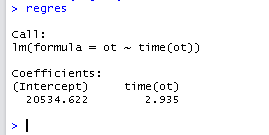
Eğrimizin y eksenini kestiği nokta 20534, ve eğimi de 2.935

Ot= 20534.62 + 2.935*<ot’nin indexi>

 

4.3. Bir Doğrusal Regresyonun Sonuçları

Bu bölümde doğrusal regresyona sadece kıyısından yaklaşacağız. Eğer “str(regres)” yazarsak, regresyon sonucunda üretilen tüm verilerin listesini de görebiliriz.

str(regres)

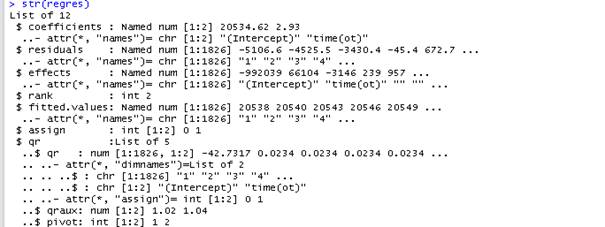
Görüldüğü üzere, regresyon sonucu, katsayılar, kalıntılar, regresyon sonucu giydirilmiş değerler ve daha bir çok veri bulunmaktadır.

“abline” komutu ile sadece doğrusal bir çizgi çektik. Ama eğer trendinden ayrılmış veriyi görmek istersek, yapmamız gereken “residuals”’a bakmak. Doğrusal regresyon için iki yöntem var:

·         resid(regres): hazır tanımlı resid komutu ile regresyon sonucu elimizde kalan kalıntıyı görebiliriz

·         eski yöntem regres$residuals komutu da aynı görevi görebilir.

Burada resid’i kullanarak, trend’den ayrışmış tüketimi görmeye çalışalım.

plot(resid(regres), pch=19,cex=0.6,col="#88000022")

 

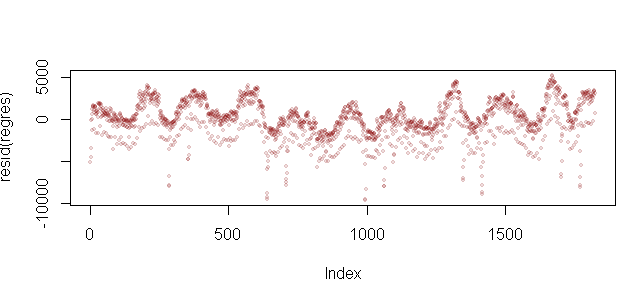
Görüldüğü üzere, verimizden trendi ayıkladıktan sonra 0’ın etrafında hareket eden bir veri setimiz oldu. Böylelikle hem verimizi artan eğilimden arındırmış olduk, hem de üzerinde çalışabileceğimiz bir veri seti elde ettik. Tabii şimdilik!!

Daha önce yaptığımız gibi, önce bir histogramına bakalım

hist(resid(regres),breaks=100)

 

 

Verimiz tam normal değil, ama ortalaması 0 olacak şekilde bir eğri elde ettik.

 

4.4. Herşeyi Bir Arada Çizdirmek

Çizdirdiğimiz iki grafiğe bakarsanız ilki 15000 ile 35000 civarında dolaşan, trendi olan bir veri iken, ikinci grafikte veriden trendini aldıktan sonra elimizde kalan 0’ın etrafında dolaşan bir veri setimiz oldu.

Soru: İki veriyi nasıl bir arada çizdireceğiz?

Cevap: Þu anda plot komutunu kullandığımızdan, ilk grafiğimizi daima plot ile çizip, sonra üzerine noktalar eklemek için “points”, çizgiler eklemek için “lines” komutunu kullacağız.

Burada dikkat etmemiz gereken şey, plot komutuna “ylim” girerek y ekseni limitlerini belirleyeceğiz. Yoksa ikinci grafiğimiz çizilmez.

plot(veri$ortalama_tuketim, pch=19,cex=0.6,col="#00008822",ylim=c(-10000,37000))

abline(regres)

points(resid(regres),pch=19,cex=0.5,col="88000088")

               

 

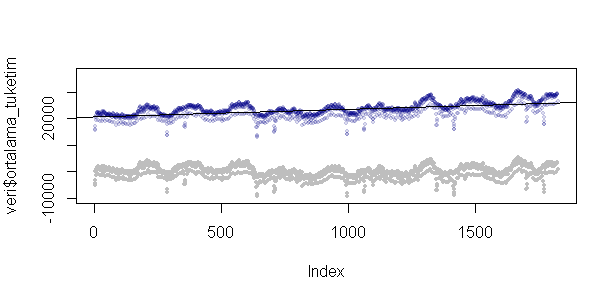
DİKKAT: Eğer bu grafiği ilk “plot” komutundaki “ylim=c(-10000,37000)” yani y eksen limitlerini -10000 ile 37000 arasında tanımlayıp sisteme girmezseniz ikinci grafiği göremezsiniz. Çünkü eksen alanının dışında kalacaktır. İki grafiği çizerken bu hususlara dikkat ediniz.

Deneyelim: (ekseni 0 ile 37000 arasında limitleyelim , ylim=c(0,37000) …. Unutmadıysanız c komutu ile vektör oluşturuyoruz, yani tek boyutlu seri)

plot(veri$ortalama_tuketim, pch=19,cex=0.6,col="#00008822",ylim=c(0,37000))

abline(regres)

points(resid(regres),pch=19,cex=0.5,col="88000088")

 

 

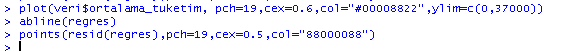
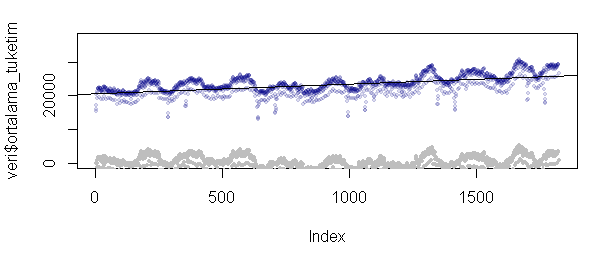
4.5. Daha Basiti de Var - Decompose

Az önceki trendi ayıklama egzersizinde birşeye dikkat ettiniz mi? Verinin ortası sanki göçmüş gibiyken, sonu da sanki ortalamanın üzerindeydi. Peki ne yapacağız?

Verimizin özelliklerine bakalım,

-          Verimiz günlük veri, 1 Ocak 2007’de başlıyor ve 31 Aralık 2011’de bitiyor.

-          365 günde bir tekrarlayan özellikleri var,

-          Aslında bir zaman serisi

O yüzden veri serimizi yani ortalama_tuketim’i ki daha sonra ot verisine atamıştık, 365 günlük frekansı olan bir veri olarak tanımlayalım.

ot_timeseries=ts(ot,frequency=365)

Þimdi çizdirelim:

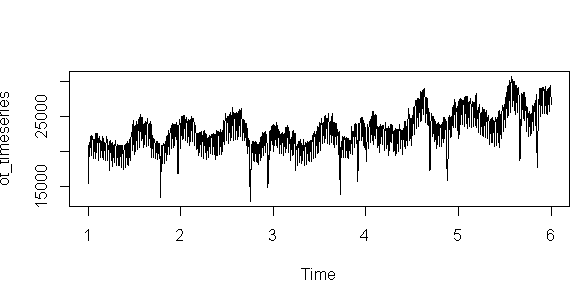
x-eksenine dikkat ettiniz mi? 1’den başladı ve 5 yıllık veriyi gösteriyor. Fakat daha anlamlı bir x-eksenine sahip olabiliriz

ot_timeseries=ts(ot,frequency=365,start = 2007)

plot(ot_timeseries)

 

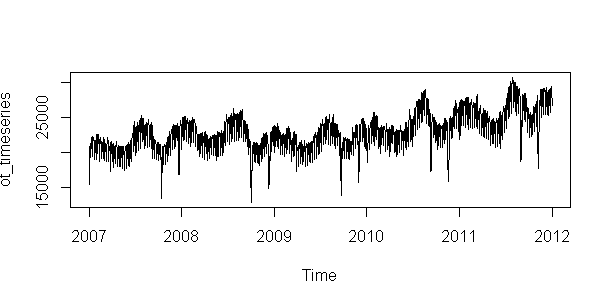
Evet verimiz 2007’den başlayan ve 365 günde bir devreden bir veriye dönüştü, ama elimizde artık yıllar sorunu kaldıJ

Bu sorunu burada bırakarak, decompose komutunun ne yaptığını görelim.

Decompose komutunun çıktısını:

ot_timeseries=ts(ot,frequency=365,start = 2007)

decompose(ot_timeseries)

görebilirsiniz. Fakat ben burada sonucu direkt olarak “plot” komutu ile çizdiriyorum. Çünkü gördükleriniz çok daha açıklayıcı olacaktır.

ot_timeseries=ts(ot,frequency=365,start = 2007)

plot(decompose(ot_timeseries))

 

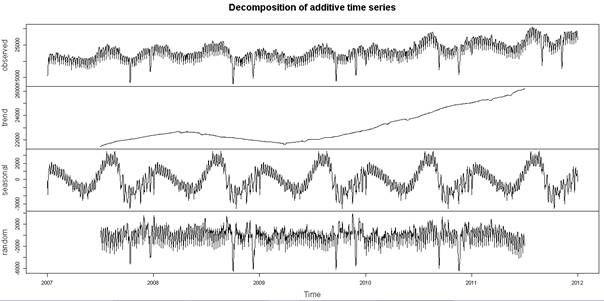
Tüm bu komutu tek satırda şu şekilde yazabilirsiniz.

plot(decompose(ts(veri$ortalama_tuketim,frequency=365)))

Daha önce düz bir şekilde ayırdığımız trend eğrisinin aslında değişken bir doğru olduğu daha doğrusu bir eğri olduğu görülmektedir. Seasonal, yani mevsimsellik ise daha tekrar eden bir veri haline gelmiştir. Ayrılamayan kısım ise, “random” başığı altında kalmıştır. Random’da her sene en az iki dip gözükmektedir. Bunlar “Kurban” ve “Ramazan” bayramlarıdır ki, bu bayramlarda talep dip yapmaktadır.

İstersek Hicri takvime göre devreden bu bayramları da mevsimselliğe kaydırabiliriz. Bunun için yapmamız gereken zaman serisinin 365 gün olan frekansını 355’e düşürmemiz işe yarayacaktır.

plot(decompose(ts(veri$ortalama_tuketim,frequency=355)))

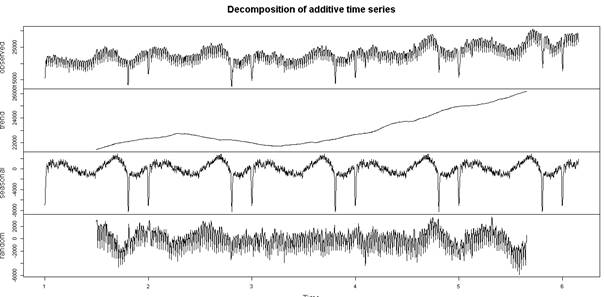
Evet frekansımızı 355’e aldığımız andan itibaren random’da olan dip değerler, seasonal’a transfer oldu.

 

4.6. Biraz Analiz

Komutlarımız bir kez daha girelim, bu sefer mavi renkle, biraz alpha değeri vererek… (Alpha değeri vermek için #RRGGBB  (R=kırmızı, G=Yeşil, B=Mavi) tarzı verinin sonuna 16’lık düzende iki basamak bir alpha değeri giriyoruz. Yani #000088 mavi rengine 88 alpha değeri veriyoruz ve #00008888 saydam bir mavi elde ediyoruz.

plot(decompose(ts(veri$ortalama_tuketim,frequency=365,start=2007)),col="#00008888")

 

 

 

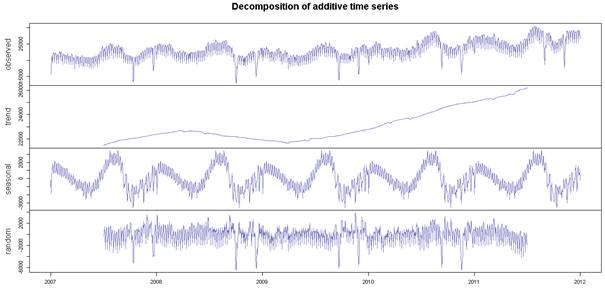
4.7. Bölüm Sonu

Bu bölümde, verimizi parçalara ayırmayı gördük. Öncelikle basit bir regresyon denemesi yaptık. Sonra da decompose komutunu kullandık. Bu arada doğrusal regresyon komutu (lm)’e kısaca bir bakış atarak, lm komutu ile verinin nasıl trendinin ayrılabileceğini gördük. Fakat sanırım decompose komutunun çok daha detaylı ayrıştırma yaptığını, bunun için de verinin periyodunu doğru tanımlamanın önemine ve ts’e (time series komutuna) değindik.

Komutlar

veri=read.csv("http://www.barissanli.com/calismalar/dersler/r/elektrik-talep.csv", header=TRUE,sep=";",dec=".")

plot(veri$ortalama_tuketim, pch=19,cex=0.6,col="#00008822")

plot(veri$ortalama_tuketim, pch=19,cex=0.6,col="#00008822")

ot=veri$ortalama_tuketim

regres=lm(ot~time(ot))

abline(regres)

regres

plot(resid(regres), pch=19,cex=0.6,col="#88000022")

hist(resid(regres),breaks=100)

plot(veri$ortalama_tuketim, pch=19,cex=0.6,col="#00008822",ylim=c(-10000,37000))

abline(regres)

points(resid(regres),pch=19,cex=0.5,col="88000088")

plot(veri$ortalama_tuketim, pch=19,cex=0.6,col="#00008822",ylim=c(0,37000))

abline(regres)

points(resid(regres),pch=19,cex=0.5,col="88000088")

ot_timeseries=ts(ot,frequency=365)

ot_timeseries=ts(ot,frequency=365,start = 2007)

plot(ot_timeseries)

ot_timeseries=ts(ot,frequency=365,start = 2007)

decompose(ot_timeseries)

ot_timeseries=ts(ot,frequency=365,start = 2007)

plot(decompose(ot_timeseries))

plot(decompose(ts(veri$ortalama_tuketim,frequency=365)))

plot(decompose(ts(veri$ortalama_tuketim,frequency=355)))

plot(decompose(ts(veri$ortalama_tuketim,frequency=365,start=2007)),col="#00008888")