R ile Enerji Analizi – Bölüm 2 – Elektrik Talebine Veri Setine Bakış 1

 

Özet : Bu bölümde, örnek bir veri seti üzerinden elektrik talebinin ilk adım analizleri yapılacaktır.

Komutlar:

a=read.csv("dosyaismi.csv",header=TRUE,sep=";",dec=".")

head (veri)

tail (veri)

str (veri)

summary (veri)

describe (veri)

mean (veri)

sd (veri)

hist (veri)

plot.new()

lines(veri)

density(veri)

 

Ders 2  - Elektrik Talebine Bakış

2.1.       Veri Dosyası / CSV dosyaları

Bu bölümde Türkiye’nin 2007-2011 yılları arasındaki talep verisinin görselleştirilmesi üzerinden bazı analizler yapılmaya çalışılacaktır.

Çalışmada kullanılacak veri seti şu adrestedir. Bu veri seti Enerji İşleri Genel Müdürlüğü Uzman Yrd. Engin İlseven tarafından hazırlanmıştır.

(Link :  http://www.barissanli.com/calismalar/dersler/r/elektrik-talep.csv )

Veri Setinin Excel’deki görünümü şu şekildedir.

Veri seti Excel formatı yerine CSV dediğimiz, virgülle veya noktalı virgülle veya tabla ayrılmış bir metin dosyası şeklindedir. Dosyayı indirdikten sonra notepad veya herhangi bir metin editörü ile de gözlemlenebilir.

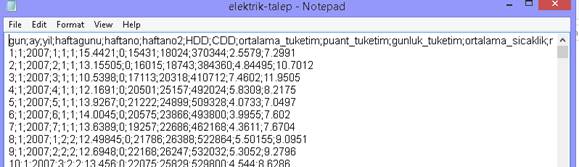
Veri setimiz görüldüğü üzere “;” ile ayrılmış sayı dizinlerinden oluşmaktadır. Türkiye’de “.” Ve “,”’ün kullanımları zaman zaman karıştırıldığı için, Türkçe kaydederken genelde “;” ile ayrım yapılmaktadır.

CSV dosyaları Excel dosyalarının aksine taşınabilir, bir çok program tarafından okunabilir metin tabanlı veri dosyalarıdır.

2.2.       Veri Dosyası İçeriği

Veri dosyamızda sırası ile :

-          Tarih bilgisi (gün, ay, yıl, haftagunu, haftano, haftano2)

-          Sıcaklık Bilgileri (HDD , CDD, ortalama sıcaklık, maksimum sıcaklık)

-          Tüketim bilgileri (Ortalama Tüketim, Puant Tüketim, Günlük Tüketim)

Sorunları minimuma indirmek için tarih dönüşümlerine girmeden gün/ay/yıl verileri ayrı ayrı sütunlar haline getirilmiştir.

Her gün için Türkiye’deki bazı şehirlerin sıcaklık değerlerinden ortalama sıcaklık, HDD, CDD değerleri hesaplanmıştır.

-          HDD: Heating Degree Days: Her bir gün için o gün sıcaklığının 17.5 Santigrad Derece’nin altında kalan kısmıdır. Kısaca ısıtma için kullanılan derece gün denir

-          CDD: Cooling Degree Days: Bu da ısıtmanın tersi olarak soğutma gün derecesi olup, o gün ki sıcaklık değeri belirli bir sıcaklığın üzerinde ise aradaki farktır.

Dolayısı ile elektrik talebinin güne, sıcaklığa bağlı değişimini hatta yıllara göre hareketini gözlemleyebileceğimiz tüm veri setleri bu listede bulunmaktadır.

2.3.       Internet’ten Veri Dosyasını Almak

Eğer veri setini sabit diskinize indirmeden kullanacak iseniz,

veri=read.csv("http://www.barissanli.com/calismalar/dersler/r/elektrik-talep.csv", header=TRUE,sep=";",dec=".")

Komutunu yazmanız yeterli!

Komut web sitemde olan elektrik-talep.csv dosyasını alarak içindekileri “veri” adlı bir R veri setine kopyalar. Bunu yaparken:

read.csv(<dosya adresi> , header = <verilerin başlığı var mı>, sep=”<ayırıcı>”,dec=”<ondalık işaret>”)

komutu bazı parametreler alır.

Bu parametreler sırası ile:

-          <dosya adresi>: CSV dosyasının sabit disk veya internetteki konumunu buraya “ işareti ile girebilirsiniz. Aynı şekilde “c:/downloads/elektrik-talep.csv” diyerek lokal bir dosyayı da kullanabilirim. DİKKAT: bölü işaretinin yönü hep sağa doğru, Linux/unix şeklinde

-          <verilerin başlığı var mı>: header=TRUE der iseniz, CSV dosyasının ilk satırını veri değil, veri etiketleri olarak algılar. Bizim dosyamızda ilk satır etiketler

-          <ayırıcı>: sep=”;” ile dosyamızda, verilerin “,” ile değil “;” ile ayrıldığını belirtiyoruz

-          <ondalık işaret> : dec=”.” İle de onlar basamağı ayırıcımızın “.” Olduğunu bildiriyoruz.

Þimdi CSV dosyasına bir kez daha baktığınızda, sıcaklık verilerinin nokta ile ayrılmış ondalıklı veriler olduğunu, binler ayıracımızın olmadığını ve tüm veri sütunlarının  “;” ile ayrıldığını görebilirsiniz.

Eğer bir sorun yok ise tüm veri setimiz artık “veri” isimli değişkende….

2.4.       Veri setimize bir bakış

Daha önce birinci derste gördüğümüz şekli ile

head(veri)

diyerek veri isimli verisetimizin ilk 6 satırına bakıyoruz. Dikkat edilirse, ilk günün 1 Ocak 2007 olduğu görülecektir.

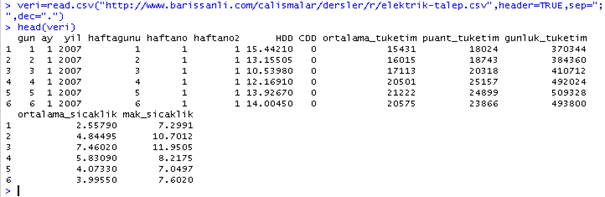
Þimdi bir de veri setimizin son satırlarına bakalım. Bunun için de kuyruk anlamına gelen tail komutunu kullanıyoruz

tail(veri)

Buradan da veri setimizin son elemanlarının 2011 yılının son günleri olduğunu rahatlıkla görebiliriz.

Peki veri setimizdeki ana başlıklar neler? Bunun için de yine bir önceki dersten hatırladığımız “ls” (LS) komutunu kullanıyoruz.

ls(veri)

2.5.       Veri setine detaylı bakış

Yukarıda  “ls(veri)” komutunu kullandığımızda, CSV dosyamızdaki tüm veri başlıklarını rahatlıkla görebildik.

Bir önceki seferde olduğu gibi $ işareti ile alt kırılımları görebileceğimiz gibi bu sefer, sayı vererekte alt kırılımlara erişebiliriz

“ls(veri)” komutunun çıktısında, sırasıyla 1 “ay” , 2 “CDD” …. ,9 “mak_sicaklik”,13 “yil” karşılığına gelmektedir. DİKKAT : ls komutu ile alfabetik dizilmiş bir “etiketler” listesine erişirsiniz. Gerçek sıra için aşağıdaki veri[0,] komutunu kullanın.

Þimdi 3 komut ile veri setimize yakından bakalım.

·         Veri setimizin genel bakış

str(veri)

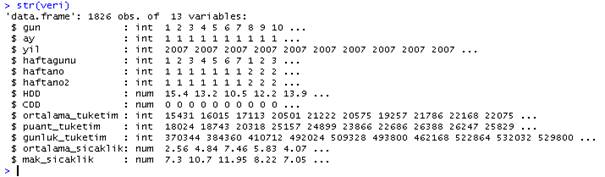
str komutu ile, veri setimizdeki tüm verilerin özelliklerini, cinslerini (tamsayı, ondalık vs) ve ilk 5-6 varisini görebiliyoruz. Yukarıdaki komutta en üst satırda:

-          Verimizin bir data.frame olduğu

-          13 değişkenin her biri için 1826 ayrı gözlem olduğu

-          “$” işaretinden sonraki kısım için de değişkenlerin isimlerini görebiliriz.

 

 

·         Aynı şekilde etiketlerimizin sırasını daha kolay okuyabileceğimiz şekilde görebiliriz.

veri[0,]

 

Burada görüldüğü üzere ilk verimiz gün, 2 ay, 3 yıl, 4 haftagunu ….. 11 gunluk_tuketim,… , 13 mak_sicaklik değerlerine denk gelmektedir.

 

Peki veri[0,] ne demektir: Bir veri seti, aynen excel deki veriler gibi hafızada bir satır ve sütun lokasyonu ile tutulmaktadır. R’da veri setleri

 

Veriseti [ satır, sütun] şeklinde tutulmaktadır.

 

Eğer satır veya sütun yerine rakam girmeyip boş bırakılırsa o satır veya sütun’daki tüm verileri ekrana gelecektir.

 

Yani veri[0,] ile etiket satırındaki tüm sütunlar ekrana gelmektedir. HATIRLATMA: R’da 0 genel de etiket satırı, verilerde genelde 1inci lokasyondan itibaren dizilmeye başlar.

 

Mesela, etiket satırlarından 3’ten 6’ya kadar olan kısmı görelim

 

Burada satır numarasını girdikten sonra, iki sütun arasındaki tüm verileri görmek için “:” işareti ile <ilk sütun>:<son sütun >  şeklinde görmek istediğimiz kısımları girebiliriz.

 

·         Tüm bu satırların istatistiksel özelliklerini görmek için ise  “summary” komutu yeterli olacaktır.

 

summary(veri)

 

 

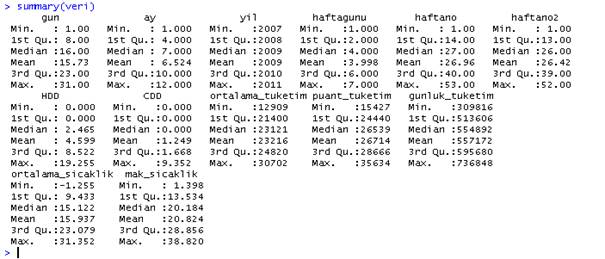
Summary komutu ile bir verisetinin tüm elemanlarının istatistiksel özelliklerini tek seferde ekrana dökebiliriz.

 

Örneğin, ısıtma kullanılan günlerin en soğuğunda (HDD , Max.)  19.25 derecelik bir ısıtma ihtiyacı olduğu, ama soğutma ihtiyacı olan günlerde ise (CDD, Max.) 9.352 derecelik bir soğutma ihtiyacı olduğu görülebilir.

 

 

2.6.       Veri Erişimi – Tekrar

Veri setlerindeki özetleri gördükten sonra, şimdi 7. Sütunda yer alan HDD alt verisine hem “$” ile hem de sayı ile erişelim.

head(veri$HDD)

head(veri[,7])

Görüldüğü üzere iki komutta aynı sonucu verdi. Çünkü her iki komutta da aynı lokasyonda olan verileri:

-          “$” ile ismen belirterek : veri$HDD şeklinde

-          Sütun numarasını vererek : veri[,7]

olarak belirttik.

Yine aynı şekilde iki ayrı sütundaki ilk 6 veriyi şu şekilde çekebiliriz.

Þimdi yine aynı sütunun istatistiksel özetlerini bir kez daha isteyelim

summary(veri$HDD)

 

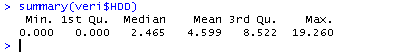
2.7.       Veri Erişimi – Ortalama ve Aralıklar

Þimdi ise verisetimize daha detaylı bakabileceğimiz bir komuta göz atalım. Bu komut ile tıpkı summary’de olduğu gibi her bir sütun için ortalama ve aralıklardaki dağılımlara kısaca bakabiliriz.

describe(veri)

 

Burada ekrana sığmamasına rağmen, mesela “Ortalama Tüketim” için de bir özet üretebiliriz.

Þimdi “describe(veri$”  yazdıktan sonra “TAB Tuşuna” (genelde Caps Lock’un üstündeki tuştur), basınca, veri’deki tüm alt değişkenlerimiz gözükmektedir.

 

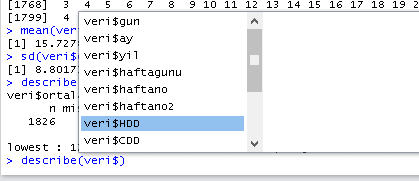
Buradan aşağı inerek ortalama tüketim verisine erişebiliriz.

 

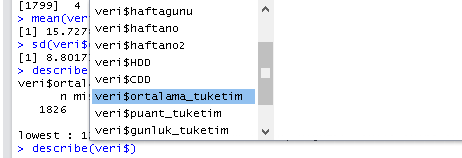
Enter’a bastığımızda da  veri$ortalama_tuketim için değikenlerimizi görebiliriz.

describe(veri$ortalama_tuketim)

Aynı şekilde veri setimizin ortalamasını mean, standart sapmasını da sd komutu ile hesaplatabiliriz.

mean(veri$ortalama_tuketim)

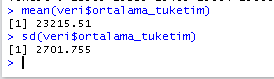
sd(veri$ortalama_tuketim))

2.8.       Histogram – Frekans Dağılımı

Verileri bu şekilde görmek oldukça faydalı olmasına rağmen, veri setlerinin istatistiksel özelliklerini grafiksel olarak görmekte çok işe yarayacaktır. Histogram kısaca frekans dağılımını göstermektedir.

Örneğin: ortalama_tuketim sütununun histogramını görmek için

hist(veri$ortalama_tuketim)

 

 

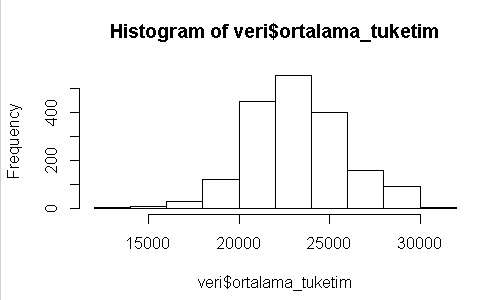
Komutunu yazmak yeterli olacaktır.  Eğer blokların aralığını beğenmiyor isek, “break” parametresi ile daha çözünürlüğü yüksek bir grafik elde edebiliriz

hist(veri$ortalama_tuketim,breaks=200)

 

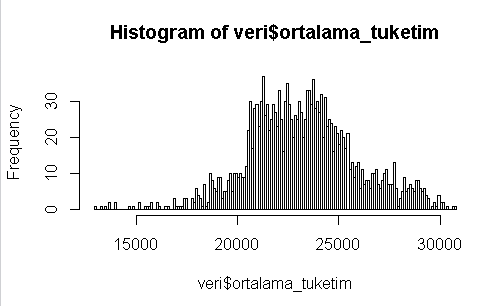
Yukarıdaki veriye baktığımız zaman aslında ortalama tüketimin neredeyse 5000 MW’lık bir alana sıkıştığını görebiliriz.

Hist komutu ile ilgili dikkat edilmesi gereken en önemli konu ise y-ekseninde genelde hep frekanslar olmasıdır. Yani olasılıklar değil frekanslar vardır. Eğer y-eksenini frekanslar yerine olasılıklar olarak göstermek istersek prob=TRUE parametresi ile kullanmamız gerekir.

hist(veri$ortalama_tuketim,breaks=200, prob=TRUE)

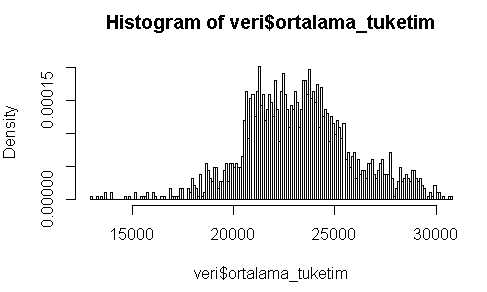
Görüldüğü üzere bir y-ekseni artık “density” yanı olasılıklarıgöstermektedir.

Bir başka histogram elde etme şekli de lines komutudur. DİKKAT: Lines komutu density ile kullanılacak olup, önce ekranı temizlemeniz gerekir.

2.9.       İki Yılın Ortalama ve Maksimum Talep Yapılarının Farkını Görme – lines ve density komutları

Peki histogramımız üzerine bir de çizgi grafiği koymak istersek bunu nasıl yapacağız?

Önce her halükarda ekranı temizleyeceğiz, sonra histogramımızı çizdirip, daha sonra da lines komutu ile  üzerine çizgileri ekleyeceğiz.

plot.new()

hist(veri$ortalama_tuketim,breaks=200, prob=TRUE)

lines(density(veri$ortalama_tuketim), col="blue", lwd=2)

 

 

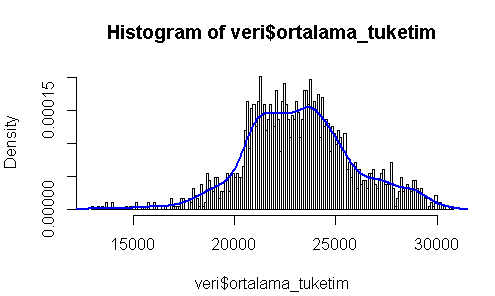
Evet, bu aşamada, veri setimizi hem histogram hem de çizgi grafik olarak üst üste yazdırabildik.

Fakat dikkat edilmesi gereken birkaç nokta var.

-          lines komutu kendisine girilen parametrelerden bir çizgi grafiği oluşturur

-          daha önce görmediğimiz lwd=2 ile (line width-çizgi kalınlığı) 2 piksel kalınlığında bir çizgi ürettik

-          col=”blue” ise ingilzce color ve blue yani renk ve mavi kelimelerine denk gelir kısaca çizgi rengi mavi olsun dedik.

-          Asıl burada çizgi üzerindeki noktaların x ve y koordinatlarını “density” komutu vermektedir.

Yani sadece (DIKKAT: density fonksiyonu tam olarak olasılık değil “kernel density” hesaplamaktadır)

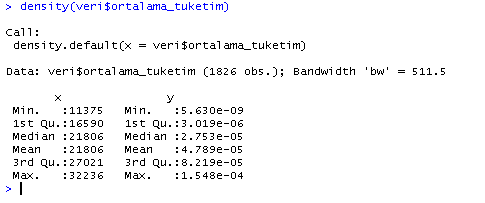
density(veri$ortalama_tuketim)

 

yazarak bir x ve y serisi oluşturuyoruz, x ekseni yine aynı histogramdaki gibi ortalama günlük tüketimler, y ekseni de bu tüketim değerlerinin olasılığına denk gelmektedir.

 

 

Þimdi yapacağımız ise ortalam tüketim histogramının üzerine puant yani günlük maksimum tüketimleri giydirmek olacak

plot.new()
hist(veri$ortalama_tuketim,breaks=200, prob=TRUE, xlim=c(15000,38000)) lines(density(veri$puant_tuketim), col="blue", lwd=2)

 

 

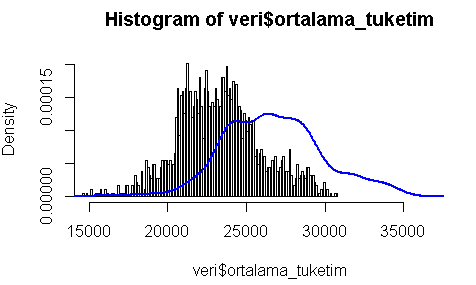
Görüldüğü üzere Ortalama tüketim ile puant tüketim arasında bir “faz kayması” yani puantın biraz sağa kaymış olduğu görülmektedir. Peki ama puant ile ortalama tüketim arasında nasıl bir fark vardır. Þimdi bunu bulmaya çalışacağız

2.10.    İlk Analiz – Ortalama Tüketim ve Puant Tüketim arasındaki fark

Bu analizi yapmak için öncelikle herm ortalama tüketimi hem de puant tüketimi aynı ortalama değer noktalarına getirmeye çalışacağız. Bunun için

1.      Önce ortalama tüketim ve puant tüketim ortalamalarını alacağız

2.      Aradaki fark kadar ortalama tüketime ekleyeceğiz

3.      Her ortalama tüketimi hem de puant tüketimi çizgi şeklinde üst üste çizdireceğiz.

Önce verileri uzun uzun yazmak yerine onları birer daha basit isimli değişkene kopyalayalım. Ortalama Tüketim yerine ot, puant tüketim yerine pt diyelim

Þimdi ise,

Ortalama Tüketim (ot) ve Puant Tüketim(pt) yi karşılıklı çizdirelim.

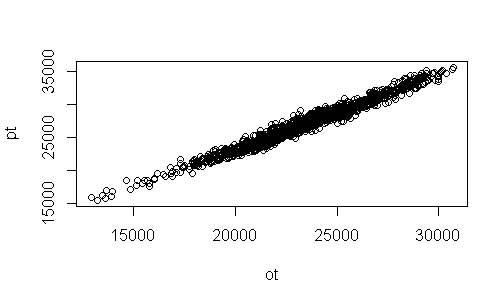
Görüldüğü üzere aradaki ilişki doğrusal olmasına rağmen, ilk dersten öğrendiğimiz şekilde, veri noktalarını kapalı ve saydam yapalım. Birkaç denemeden sonra saydamlık değerini biraz küçüklterek aşağıdaki grafiği elde ederiz

 

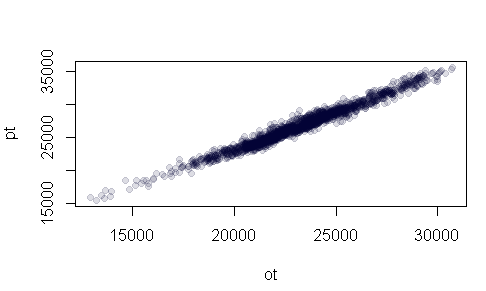
Görüldüğü üzere arada linear bir ilişki var. Bu ilişkinin eğimini bulmak içinde pt/ot’ye bölüp ortalamasını alacağız.

Bunun için önce bir “oran” değişkenine pt/ot oranını atıyoruz. Oran değişkeni aslında her bir satır için pt değerinin ot değerine bölümüdür. Bu yüzden aşağıdaki komut bize oran’ın grafiğini verecektir.

plot(oran)

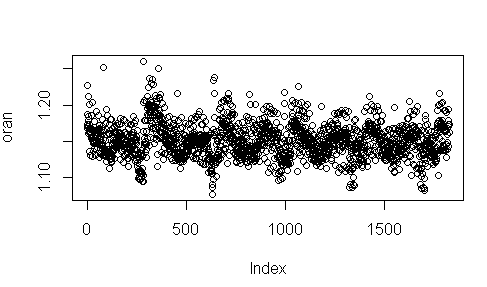
mean(oran) komutuyla da, Puant Tüketimin Ortalama Tüketime oranının 1.15 olduğunu görüyoruz.

mean(oran)

yukarıdaki grafiğe bir dakika bakmakta fayda var. Çünkü, puant talebin ortalama talebe oranında bir mevsimsellik, bir dönemsellik gözükmektedir, bu ise başka bir bölümün konusudur.

Sonucunda bu bölüm için ortalama tüketimi 1.15 ile çarparsak puant talebe göre bir anlamda normalize etmiş olacağız.

 

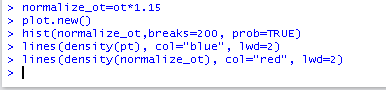
Önce ot’yi 1.15 ile çarparak normalize_ot elde edelim

normalize_ot=ot*1.15

Ardından ekranı temizleyelim

plot.new()

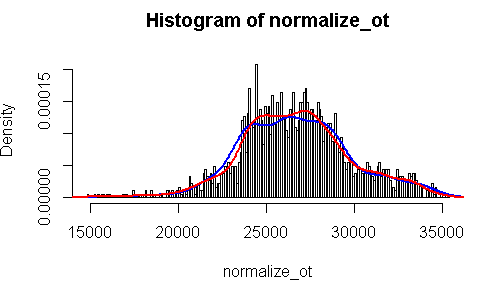
şimdi önce normalize ortalama tüketim histogramımızı, sonra puant ve ortalama tüketimin çizgi grafiklerini üst üste yerleştirelim.

hist(normalize_ot,breaks=200, prob=TRUE)

lines(density(pt), col="blue", lwd=2)                        # puant talep mavi renk

lines(density(normalize_ot), col="red", lwd=2)      # normalize ortalama tüketim kırmızı renk

 

Gördüğümüz bir şey var, puant verisi ortalama tüketim verisine göre daha sivri, kurtosis’i daha pozitif.

 

 Bu bölümdeki komutlar

veri=read.csv(“http://www.barissanli.com/calismalar/dersler/r/elektrik-talep.csv” ,header=TRUE , sep=";" ,dec=".")

head(veri)

tail(veri)

ls(veri)

veri["1"]

veri[1]

ls(veri)

veri$CDD

head(veri$CDD)

ls(veri)

head(veri$HDD)

head(veri[8])

head(veri[2])

head(veri[1])

head(veri[2])

dir(veri)

head(veri)

ls(veri,pos = TRUE)

ls(veri,pos = FALSE)

?ls

str(veri)

summary(veri)

veri[,:1]

veri[:1]

veri[,1]

veri[1,]

veri[0,]

veri[0]

veri[0,]

veri[0,]

str(veri)

veri[0,]

veri[0,3:6]

summary(veri)

?summary

str(veri)

veri$HDD[1:6]

veri[7][1:6]

veri$HDD[1:6]

veri[7,1:6]

veri$HDD[1:6]

veri[1:6,7]

head(veri$HDD)

head(veri[,7])

summary(veri$HDD)

hist(veri$HDD)

hist(veri$CDD)

hist(veri$CDD,breaks=400)

describe(veri)

?describe

sd(veri)

mean(veri)

mean(veri[1:,])

mean(veri[,1:10])

mean(veri[1:10,])

mean(veri2[1:10,])

mean(veri2[1:10,1:10])

veri$gun

mean(veri$gun)

sd(veri$gun)

describe(veri$ortalama_tuketim)

describe(veri$ortalama_tuketim,)

describe(veri$ortalama_tuketim)

mean(veri$ortalama_tuketim)

sd(veri$ortalama_tuketim)

hist(veri$ortalama_tuketim)

hist(veri$ortalama_tuketim,breaks=200)

density(veri$ortalama_tuketim)

hist(veri$ortalama_tuketim,breaks=200, prob=TRUE)

plot.new()

hist(veri$ortalama_tuketim,breaks=200, prob=TRUE)

plot.new()

hist(veri$ortalama_tuketim,breaks=200, prob=TRUE)

lines(density(veri$ortalama_tuketim), col="blue", lwd=2)

plot.new()

lines(density(veri$ortalama_tuketim), col="blue", lwd=2)

plot.new()

hist(veri$ortalama_tuketim,breaks=200, prob=TRUE)

lines(density(veri$ortalama_tuketim), col="blue", lwd=2)

density(veri$ortalama_tuketim)

?density

a<-density(veri$ortalama_tuketim)

sum(a)

sum(a$y)

sum(a$x)

plot.new()

hist(veri$ortalama_tuketim,breaks=200, prob=TRUE)

lines(density(veri$puant_tuketim), col="blue", lwd=2)

plot.new()

hist(veri$ortalama_tuketim,breaks=200, prob=TRUE, xlim=c(15000,38000))

lines(density(veri$puant_tuketim), col="blue", lwd=2)

plot.new()

lines(density(veri$puant_tuketim), col="blue", lwd=2)

plot.new()

hist(veri$ortalama_tuketim,breaks=200, prob=TRUE, xlim=c(15000,38000))

lines(density(veri$puant_tuketim), col="blue", lwd=2)

ot<-veri$ortalama_tuketim

pt<-veri$puant_tuketim

mean(ot)

mean(pt)

sd(ot)

sd(pt)

plot(ot,pt)

plot(ot,pt,pch=19)

plot(ot,pt,pch=19,col=veri$yil)

plot(ot,pt)

plot(ot,pt,pch=19,col="#00003366")

plot(ot,pt,pch=19,col="#00003322")

ot/pt

oran=pt/ot

mean(oran)

oran=pt/ot

plot(oran)

mean(oran)

normalize_ot=ot*1.15

plot.new()

hist(normalize_ot,breaks=200, prob=TRUE)

lines(density(pt), col="blue", lwd=2)

lines(density(normalize_ot), col="red", lwd=2)